この問題は,つぎのように定めることで,解決される: 《行列式が定める「平行四辺形の面積」は,符合のついた平行四辺形の面積》 即ち,行列式 det( (a 11, a 12), (a 21, a 22) ) の値の正負は,つぎのようになる: 平行四辺形の中を,原点中心に,(a 11, a 12) を (a 21, a 22) に向けて回転する。 回転T 次にウの考えを説明してください。 (省略) T 面積の同じ「平行四辺形に変える方法」だね。違う平行四辺形に変えた人もいました。 さんはどんな平行四辺形にしたのかな。(変形の仕方が違う考えを3面積 31平行四辺形の面積 32三角形の面積 33台形の面積 34ひし形の面積 35円の周の長さと面積 4整数 41偶数と奇数 42倍数と公倍数 43約数と公約数

無料 中2数学 発展問題 解答プリント 233 平行四辺形4
平行 四辺 形 面積 問題
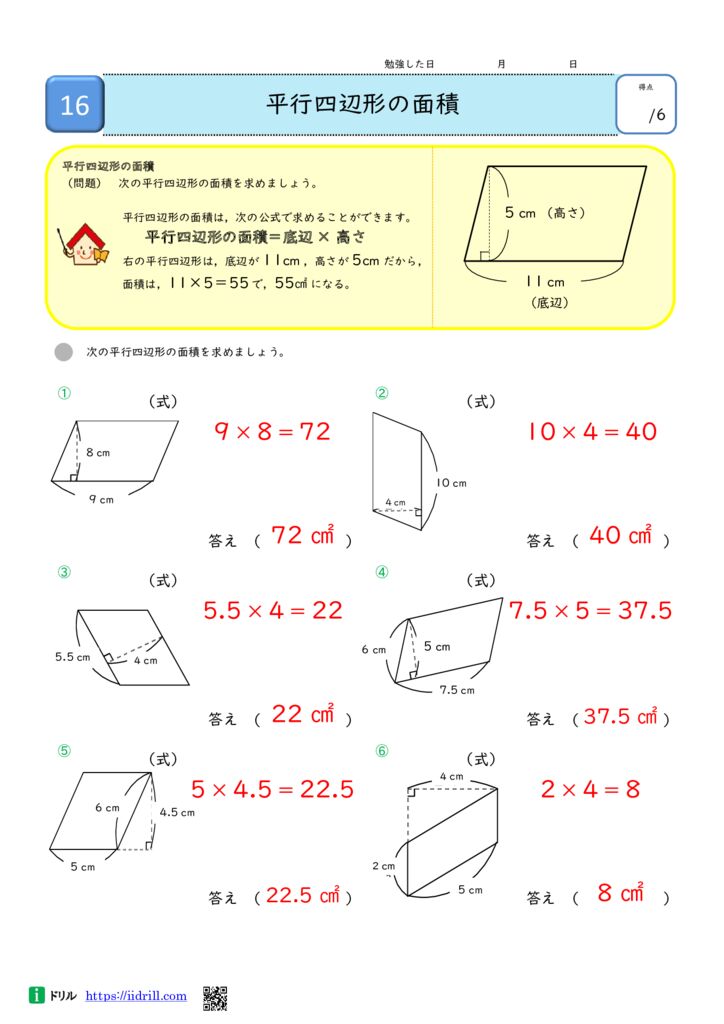
平行 四辺 形 面積 問題-解答 平行四辺形の面積は 平行四辺形の面積=底辺×高さ÷2 ですね。この問題の場合,高さが与えられていない代わりに,異なる2辺とその挟む角が与えられています。よって,この2つのことがらより高さ h を求めることにしましょう。左の図より,一つの次の平行四辺形の面積を求めましょう。 問題集の無料ダウンロードサイトは「おかわりドリル」で検索 https//wwwokadorinet ©おかわりドリル ① ② ③ 6cm 7cm 8cm 3cm 3cm 2cm 4cm 4cm 5cm 5cm 7×6=42 42cm2 5×3=15 15cm2 3×2=6 6cm2 平行四辺形の面積 月 日 名前 始めた時間 終わった時間 かかった時間 次の平行




関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ
平行四辺形の角度、辺の長さを求める問題を解説! 平行四辺形の中から面積の等しい三角形を見つける問題を徹底解説! 等積変形三角形の面積問題と作図のやり方は?証明問題も紹介!←今回の記事 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる! 頑張っているの平行四辺形の面積=底辺×高さ ひし形の面積=対角線×対角線÷2 台形の面積=(上底+下底)×高さ÷2 ※台形の面積は特に忘れやすいので注意が必要です。 正方形はひし形でもあるので 正方形の面積=対角線×対角線÷2 でも求められることも覚えておくといい5年 平行四辺形の面積|算数イメージ動画集|大日本図書 平行四辺形の面積を求めるにはどうしたらいいでしょうか。 台形を2つ合わせて,あるいは三角形と台形を合わせて長方形にしてみると公式が使えます。 つまり,平行四辺形の面積は 底辺×高さ で
第118問 平行四辺形の面積の和 図形ドリル 6年生 平行四辺形 相似 面積の和 ★★★☆☆☆ (中学入試標準レベル) 思わず「お~~! ! 」と言いそうな良問を。 受験算数の定番からマニアックな問題まで。 図形ドリルでは,色々なタイプの図形問題を取り上げています。 また平行四辺形の面積は300㎠なので、 300s=300㎠ s=1㎠ と求まります。 よって、青色部分の面積は 111s=111㎠ となります。 まとめ ビジュアルに騙されて面白そうと思ったらまさかの難問でした。 ですがかなり面白い問題だと思いました。 使う知識も相似のみでその範囲を習った時な次の2つの問題は、面積の分割とは違うが、等積図形をうまく図形に組み合わせて、 1つの図形を形作るという意味で、同じ範疇の問題と考えていいだろう。 問題 一般の三角形において、同じ面積をもつ平行四辺形を作れ。
小学5年生の算数 三角形や平行四辺形の面積 問題プリント 無料ダウンロード・印刷できる、三角形と平行四辺形の面積を求める問題プリント です。 三角形と平行四辺形の公式とその考え方を確認し、面積を求める練習を繰り返し行うことができます。 平行四辺形の面積=底辺×高さ となります。 これは、長方形を移動した平行四辺形の面積(たて×横)と同じになることから考えることができます。 次のような問題がよく出題されます。底辺と高さがどこか注意して間違えないようにしましょう。 下の平行四辺形の面積を求める。 関数グラフ上の平行四辺形の座標、面積、二等分線などの問題を解説! yはxの2乗に比例する関数 kaztastudy ツイート



平行四辺形の部分面積は パズル算数クイズ



ミニトラ問題
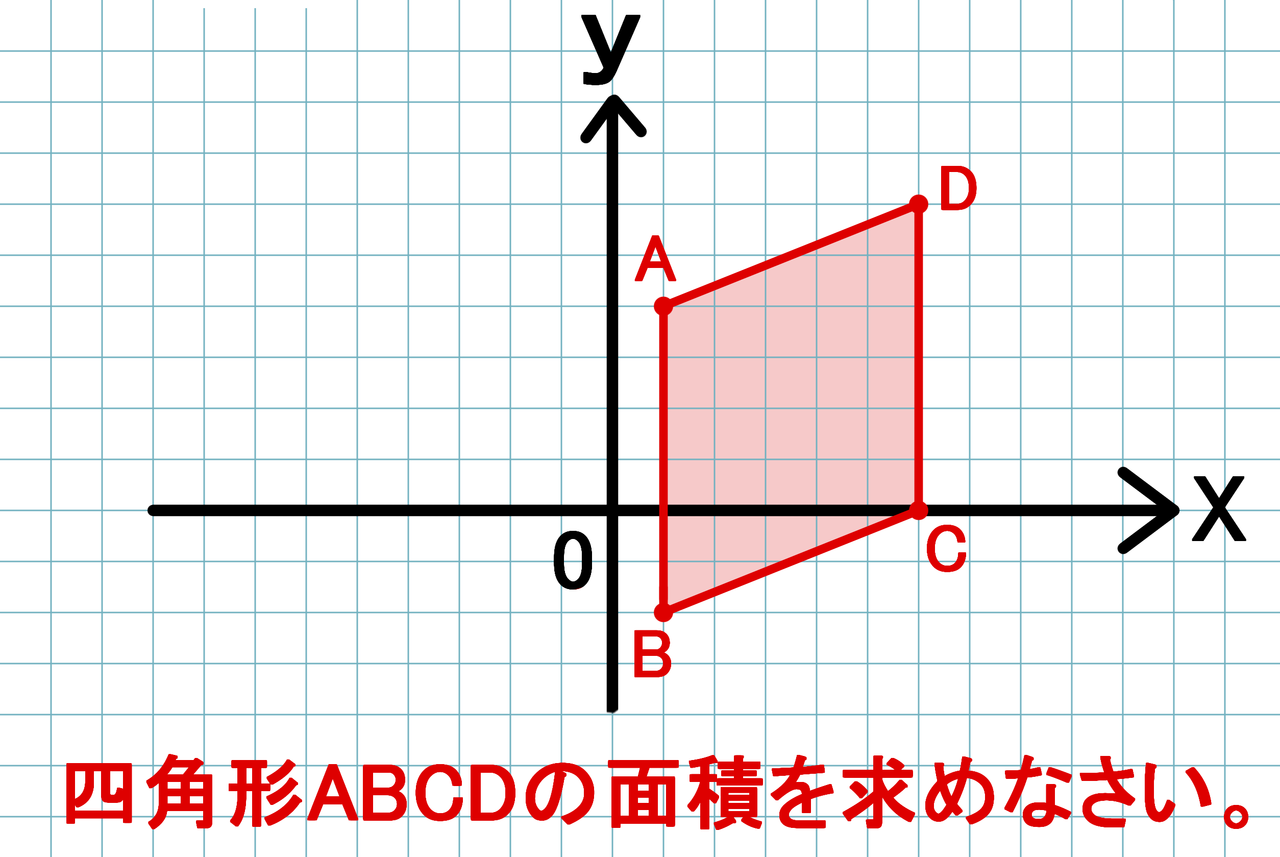
研究授業でよく見かける平行四辺形の面積の求め方の授業。 最後は、四角形の 「たて×横」 を、「 底辺×高さ」 にうまく移行できるように授業を組み立てていきたいです。2年生 5 図形の性質と証明 知識・技能の習得を図る問題 年 組 号 氏名 全国学力・学習状況調査 A問題 ④ 4 四角形は,1組の向かい合う辺が平行でその長さが等しいとき,平行四辺形になります。点 \(d\) をとります。平行四辺形 \(adbc\) の面積が \(24\) となるとき、 点 \(d\) の座標を求めなさい。 ただし、点 \(c\) の \(y\) 座標は、点 \(a\) の \(y\) 座標より大きいものとする。 解説 この平行四辺形の面積を、「底辺×高さ」から求めようとするのは 無謀ですね。




中学 数学 平行四辺形の面積の問題です 中学 数学 平行四辺形の 数学 教えて Goo
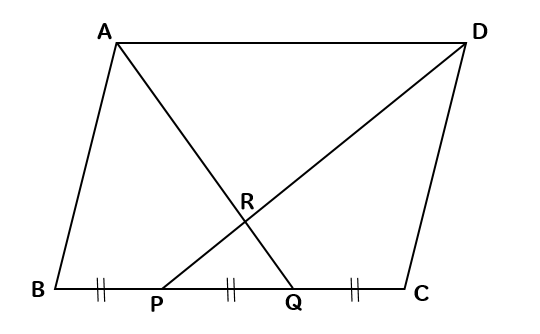



相似 平行四辺形と面積比の問題を徹底解説 数スタ
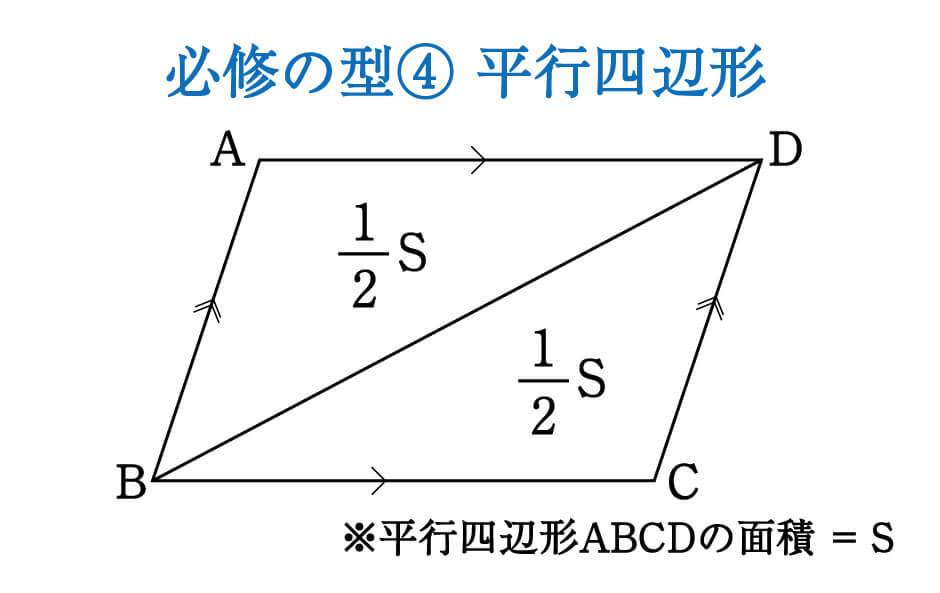
平行四辺形の性質/平行四辺形についての計算問題/平行四辺形の性質:三角形の合同/ 二等辺三角形・正三角形など /平行四辺形になる条件/平行四辺形になることの証明/ 対角線に注目/ 三角形の合同を先に証明/いろいろな四角形/面積が等しい三角形/ 面積を求める /等積変形数学25章図形の性質と証明「平行線と面積」<応用問題> 組 番 名前 1右の図において,四角形ABCDは平行四辺形です。 このとき, BCFと面積が等しい三角形をすべて 答えなさい。 2右の図のように,平行四辺形ABCDの辺BC上に点E算数 面積の学習教材・問題集です。 以下からページ番号ををご選択ください。 面積をしらべよう4 三角形・平行四辺形・ひし形・四角形定規不要 問題P001 面積をしらべよう4 三角形・平行四辺形・ひし形・四角形定規不要 問題P002 面積を
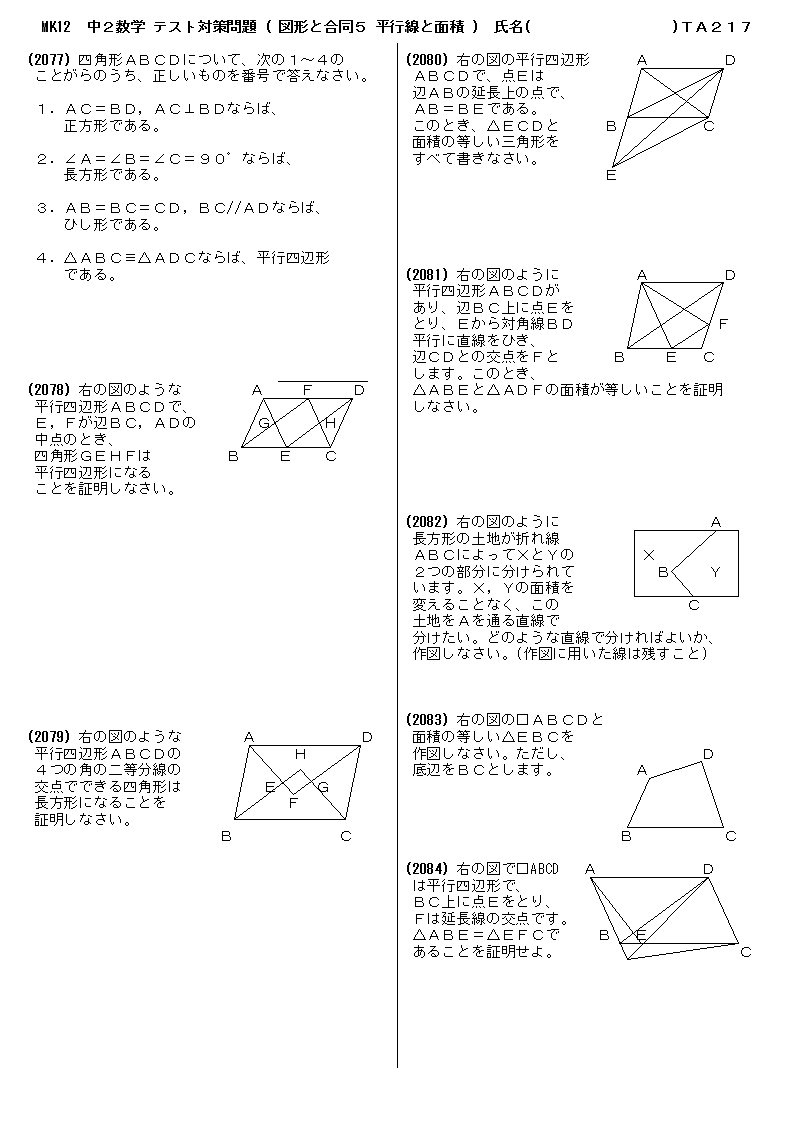



無料 中2数学 テスト対策 問題プリント 217 図形と合同5 平行線と面積
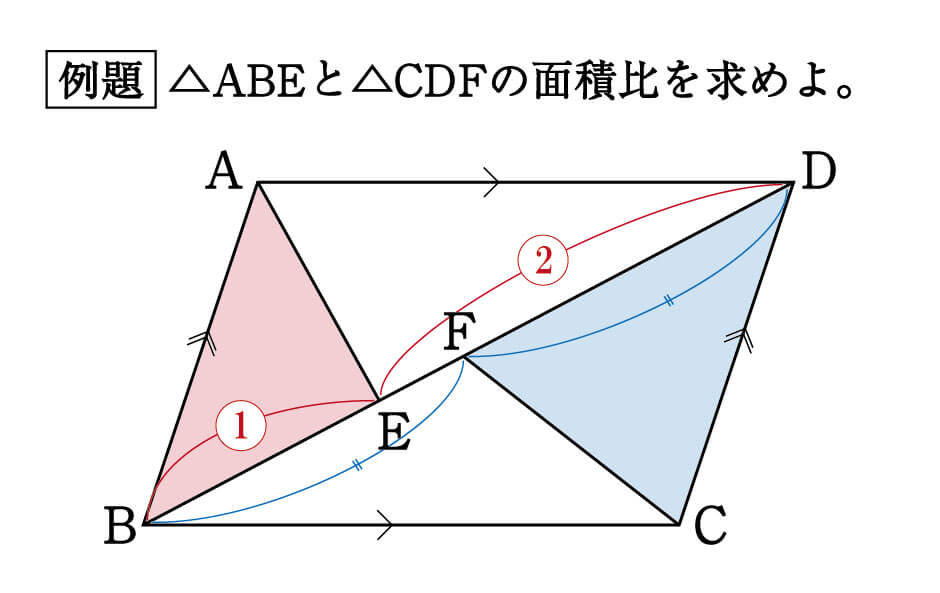



数学 なぜ面積比は苦手になりがちなの 面積比 集中特訓 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
小学校5年生で習う「平行四辺形」 の面積を求める問題集です。 問題をランダムで生成することができ、答えの表示・非表示も切り替えられます。印刷してご活用ください。 ちなみに 平行四辺形 の面積の求め方についてはこちらに詳しく説明しています。平行四辺形の証明問題 等積変形1 無料で使える中学学習プリント http//chugakumanabihirobanet/ 2 解答 DBC= DBE+ DEC 第292問 平行四辺形の面積 図形ドリル 5年生 6年生 平行四辺形 相似 相似比 面積比 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げています。



平面図形と比 平行四辺形の面積比 Next Stageのブログ
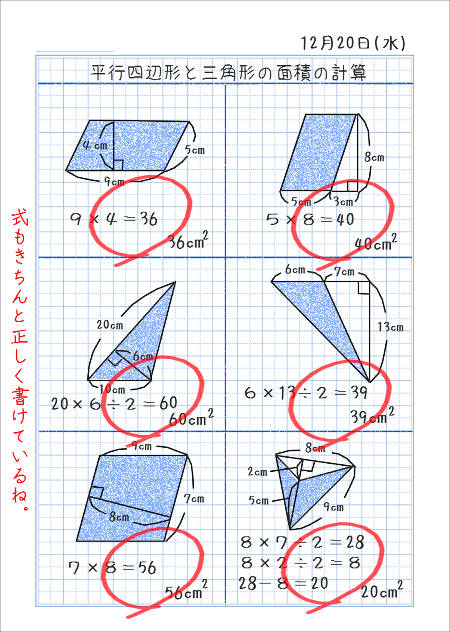



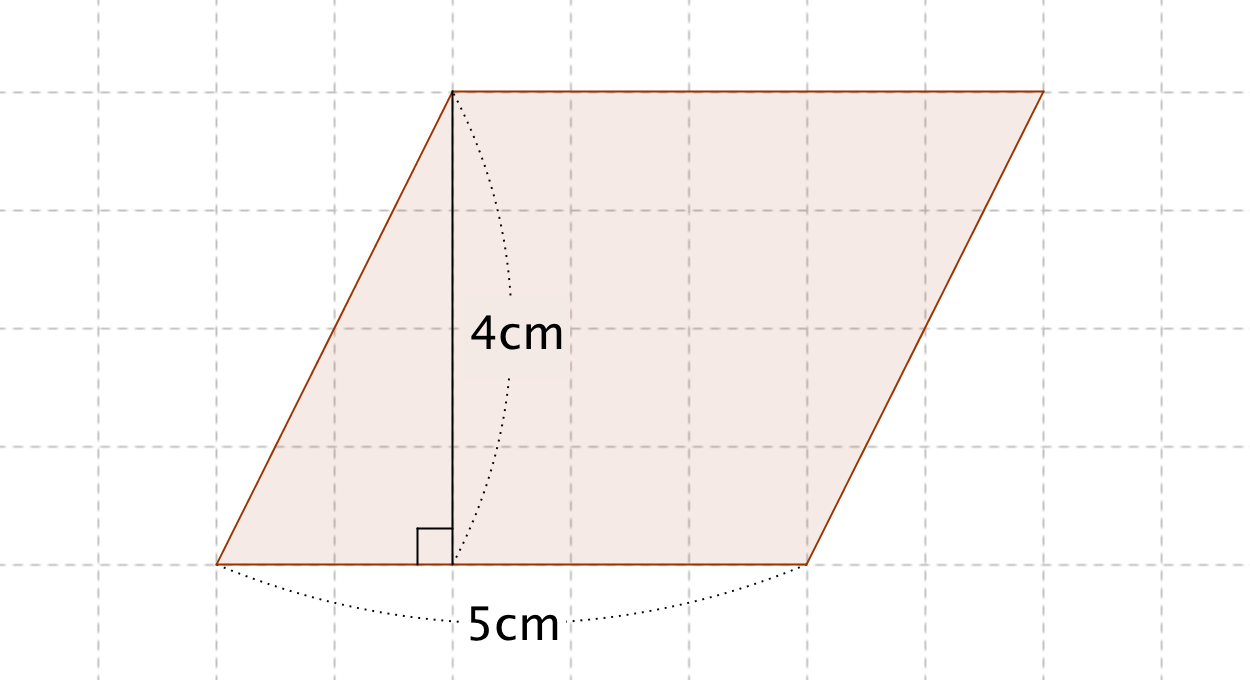
平行四辺形と三角形の面積 家庭学習レシピ
・ 面積に関する練習問題を解く。 ・ 学習内容を振り返りまとめる。 公式を使って 面積を求める ことができる。 (エ) 公式を使って 面積を求めら れることを理 解している。 (エ) 15 1つの点を長方形や平行四辺形 の中のどこにとっても上下、左右の 三角形の面積の和は等しくなるこ とを理解平行四辺形の面積=5cm×4cm=cm 2 答5. 平行四辺形の面積を求める式に数値を代入して計算してください。 平行四辺形の面積=cm×55cm=451cm 2 答6. 平行四辺形の面積を求める式を「底辺=」に変形させて計算してください。 答7. 平行四辺形は四角形なので、内角の和は360°です。 トップページへ戻る 学年別一覧(問題)へ行く 勉強をするもウ+エも正方形の面積の半分になりま 10 図のように等積変形すると、色のつい た部分はひし形の半分になります。 図のように等積変形すると、求める面 積は平行四辺形の半分になります。 12×18=216(㎠)・・・平行四辺形 2 4、6〜10から分かるように、ア+イ



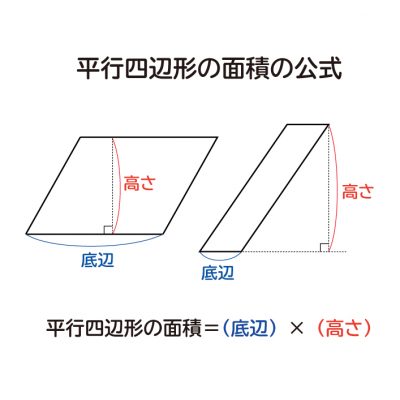
平行四辺形の面積の公式 算数の公式




平行四辺形の面積の求め方 公式と計算例
相似比の練習問題(平行四辺形1) 問1.次の各問いに答えなさい。 (ア) abcd においてae:ed =2:1 で efd の面積が2 cm 2のとき (1) cfd の面積 (2) bcf の面積 (3) abcd の面積 (イ)右の平行四辺形abcd で、辺ab の中点をe、対角線bd とce の交点をf とするとき小学5年生の算数 三角形や平行四辺形の面積の問題プリントを無料ダウンロード・印刷 (プリント5枚) 小学5年生の算数 四角形の面積 台形・ひし形ほか 問題プリント な問題が,21の都立西にあったのでご紹介します。 問1,問2中2の図形証明分野習った後に解ける 問3相似習った後に解ける 芸術的な難問高校入試 第52回 「平行四辺形の超難しい証明」 出典:令和3年度 都立西高校(独自作成校) 過去問 数学 範囲:空間図形,相似,三平方の定理,難問 難易度:★★★★★★ 美しさ:★★★★★★ <問題> <PDF




面積 上 面積の意味から 正方形 長方形 平行四辺形 三角形の面積の求 思考力算数練習張シリーズ 39 M Access 本 通販 Amazon




高校数学 平行四辺形の面積の求め方 例題編 映像授業のtry It トライイット



小学校5年 算数 面積 等積変形 問題編 パパしゅくとコラボしたよ Youtube



平行四辺形を分ける面積比の求め方 算数解法の極意
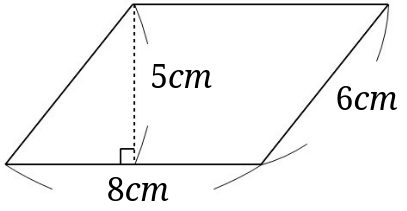



平行四辺形の面積の求め方で習う公式は なぜ底辺 高さになるの みけねこ小学校



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生
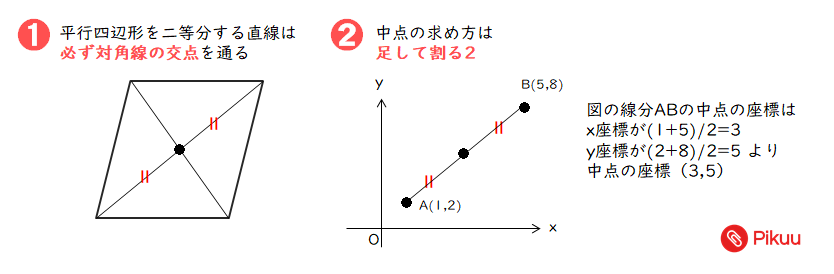



中学数学 平行四辺形の面積を二等分する直線を求める定期テスト予想問題 Pikuu
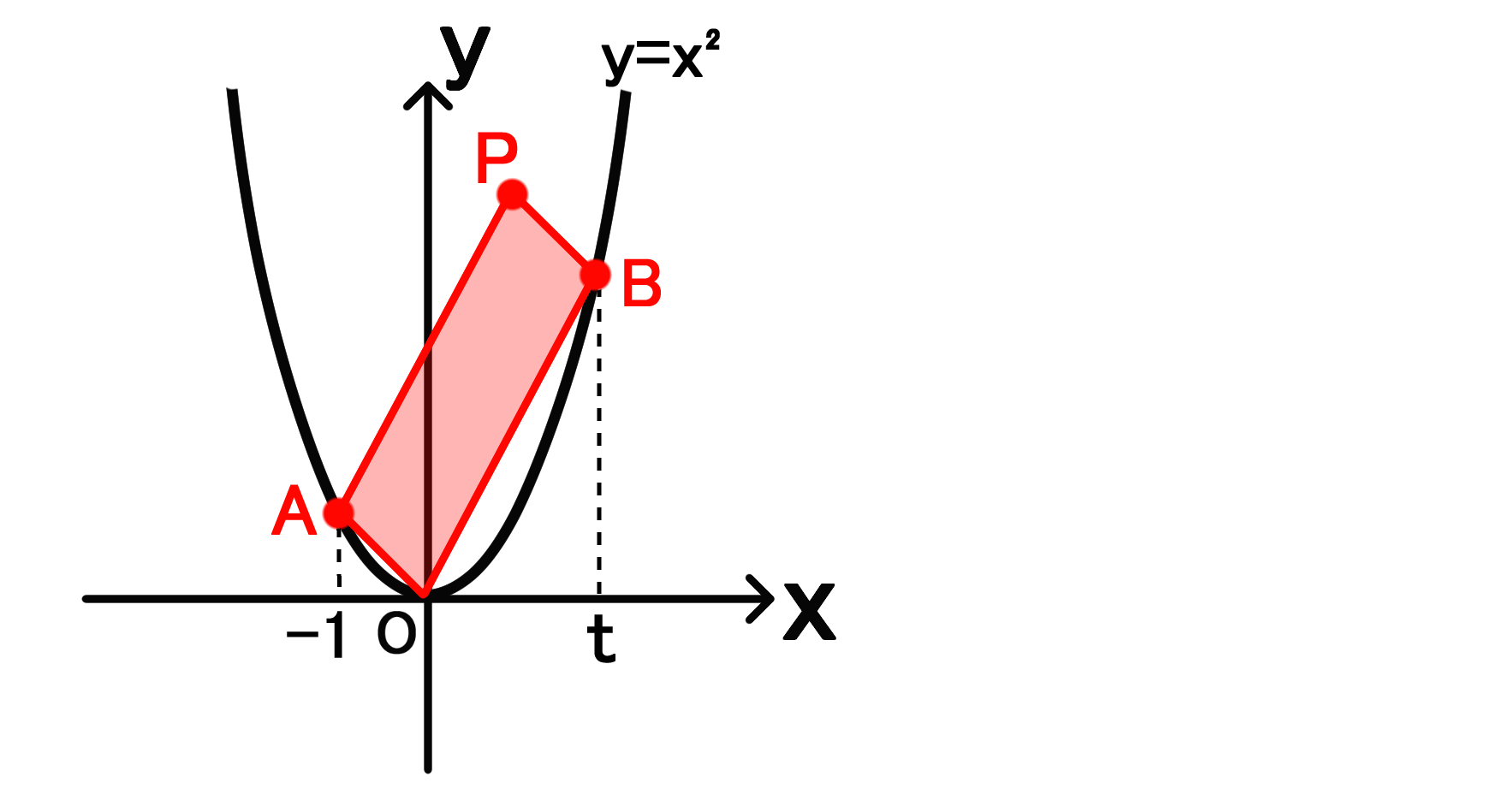



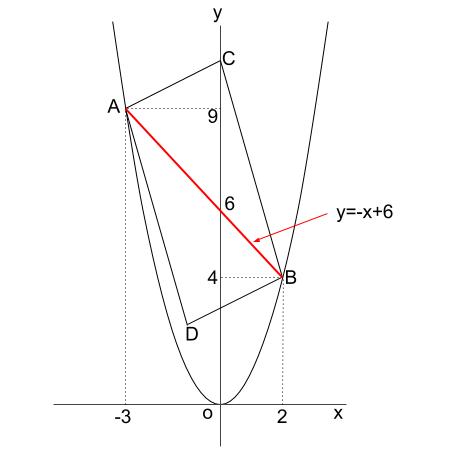
放物線y X 上の点を結ぶと平行四辺形になる問題 バカでもわかる 中学数学




数学検定準2級 2次 過去問 お願いします Clear
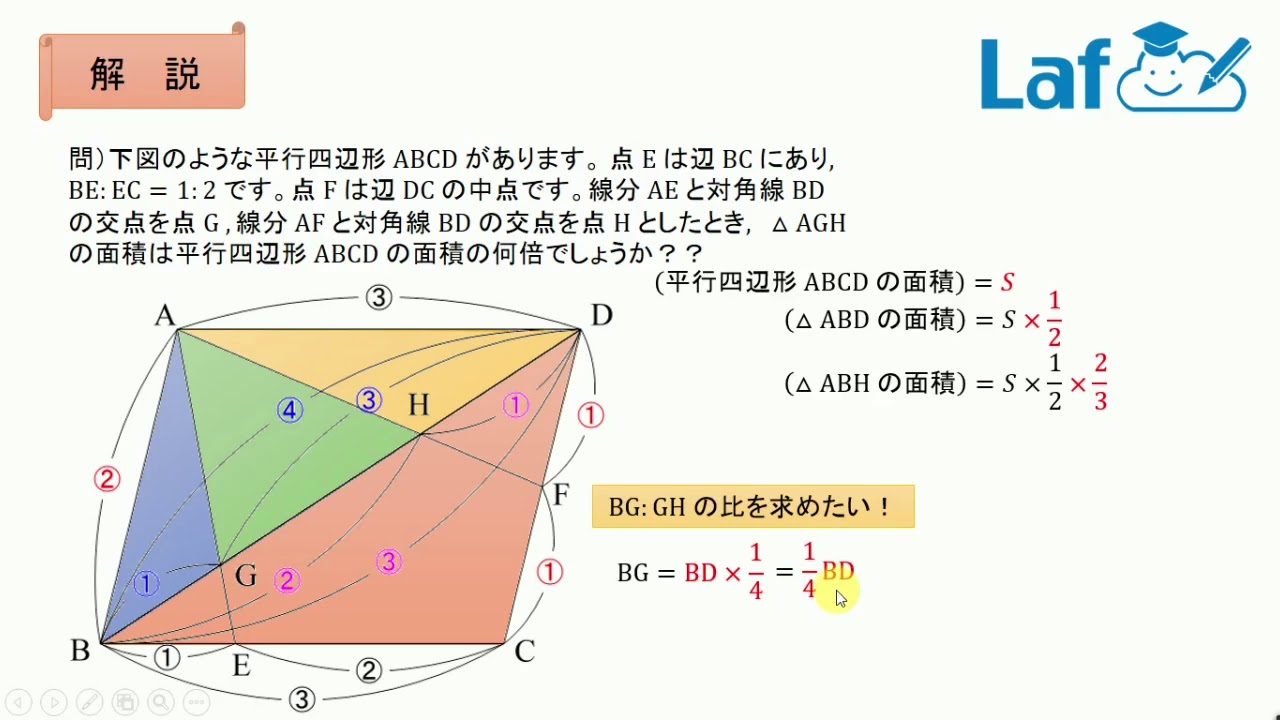



中3数学 相似な図形 三角形の面積は平行四辺形の面積の何倍 Youtube



平行四辺形abcdにおいて Baの延長上にae 4cmとなる点e Yahoo 知恵袋
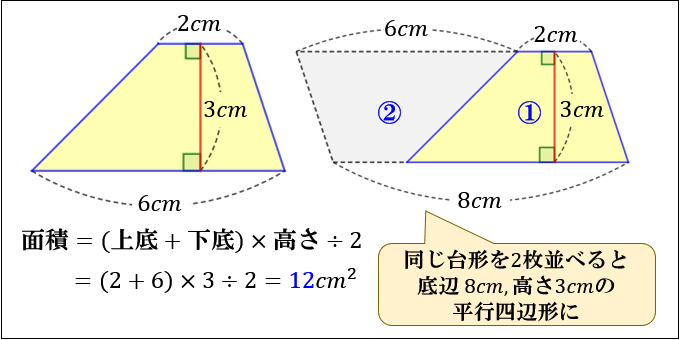



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ




ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun



3




D 2 2 Abcd Dce Descubre Como Resolverlo En Qanda




小学5年生の算数 四角形の面積 台形 ひし形ほか 問題プリント ちびむすドリル 小学生




中点連結定理とは 逆の証明や平行四辺形の問題もわかりやすく解説 遊ぶ数学



小学5年生 算数 無料問題集 平行四辺形の面積 おかわりドリル




Dfeの面積と平行四辺形の面積比の問題です Clear
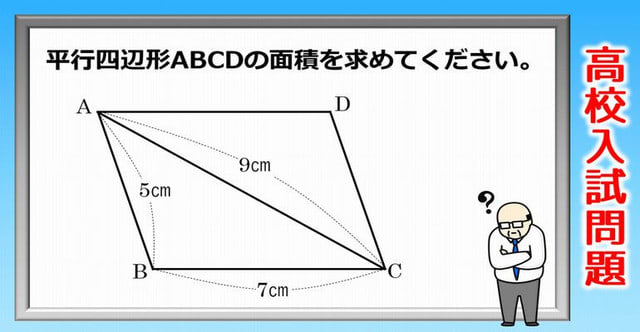



高校入試 シンプルですが悩んでしまう平行四辺形の面積の良問 暇つぶしに動画で脳トレ



平行四辺形全体の面積の何倍 大阪星光学院中学 2015 これが中学入試に出た図形問題



図形問題が驚くほど得意になる基本問題とは あおぞら塾




直撃 中学入試問題 第53回 鴎友学園女子中 面積比の問題 北辰塾 情報局




等積変形を用いる面積問題 14年 早稲田中学校 恋する中高一貫校 適性検査 徹底攻略



Q Tbn And9gct8mjpenhvsxxfek Ceorhkk1e5jnkqcmelwl1yafnkyt4mflap Usqp Cau



2乗に比例 平行四辺形の面積 中学数学の無料オンライン学習サイトchu Su




小5 算数 小5 41 平行四辺形の面積 Youtube
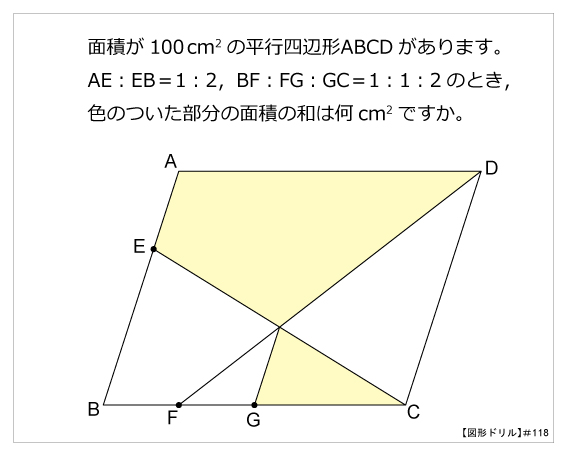



図形ドリル 第118問 平行四辺形の面積の和 算数星人のweb問題集 中学受験算数の問題に挑戦



この平行四辺形 面積の比は パズル算数クイズ




平行四辺形で知っておくべきこと 苦手な数学を簡単に



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典
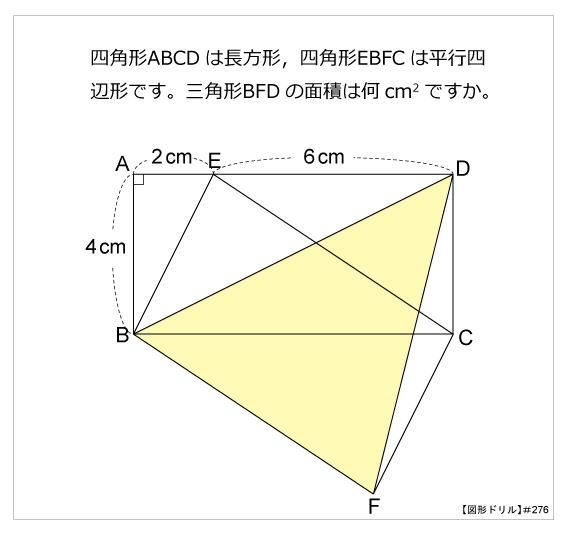



図形ドリル 第276問 長方形と平行四辺形 算数星人のweb問題集 中学受験算数の問題に挑戦




平行四辺形の面積 ベクトルでの公式 理数系無料オンライン学習 Kori



今月の問題 平行四辺形の中の三角形の問題
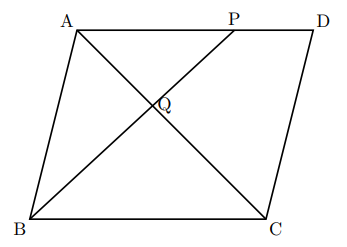



攻略法 平行四辺形と面積 数樂管理人のブログ




相似 平行四辺形と面積比の問題を徹底解説 数スタ
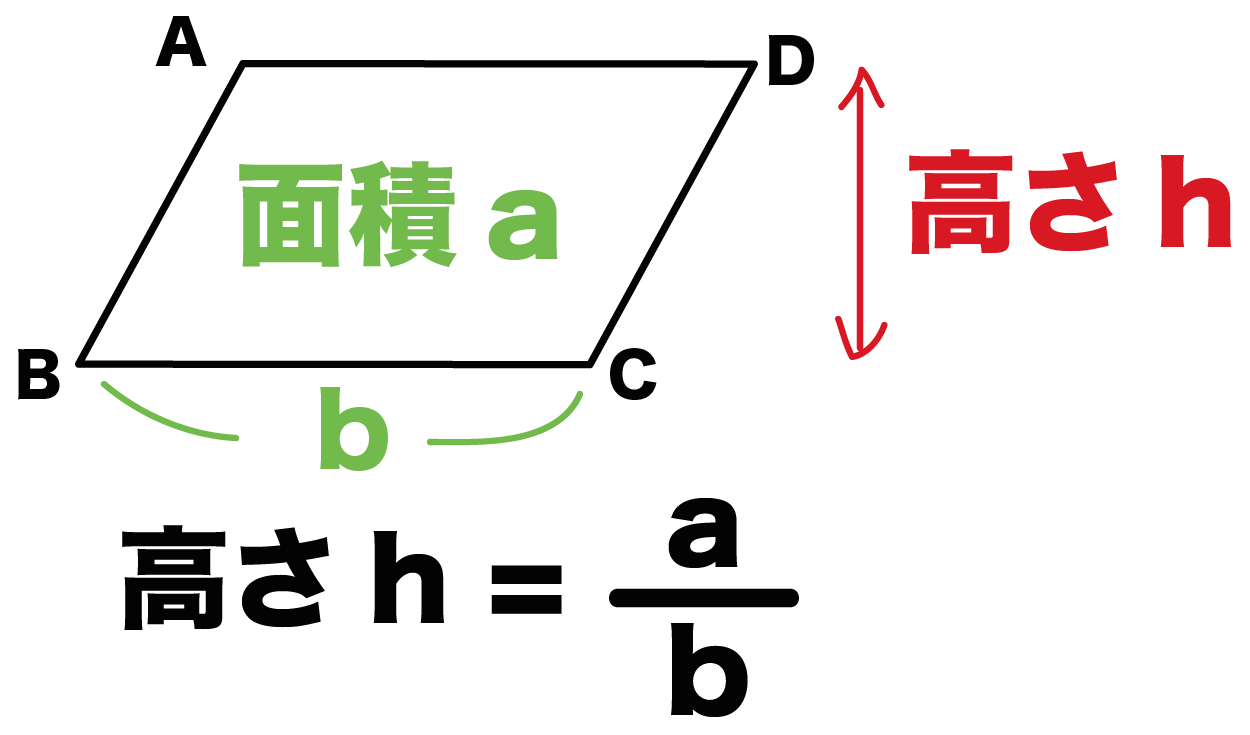



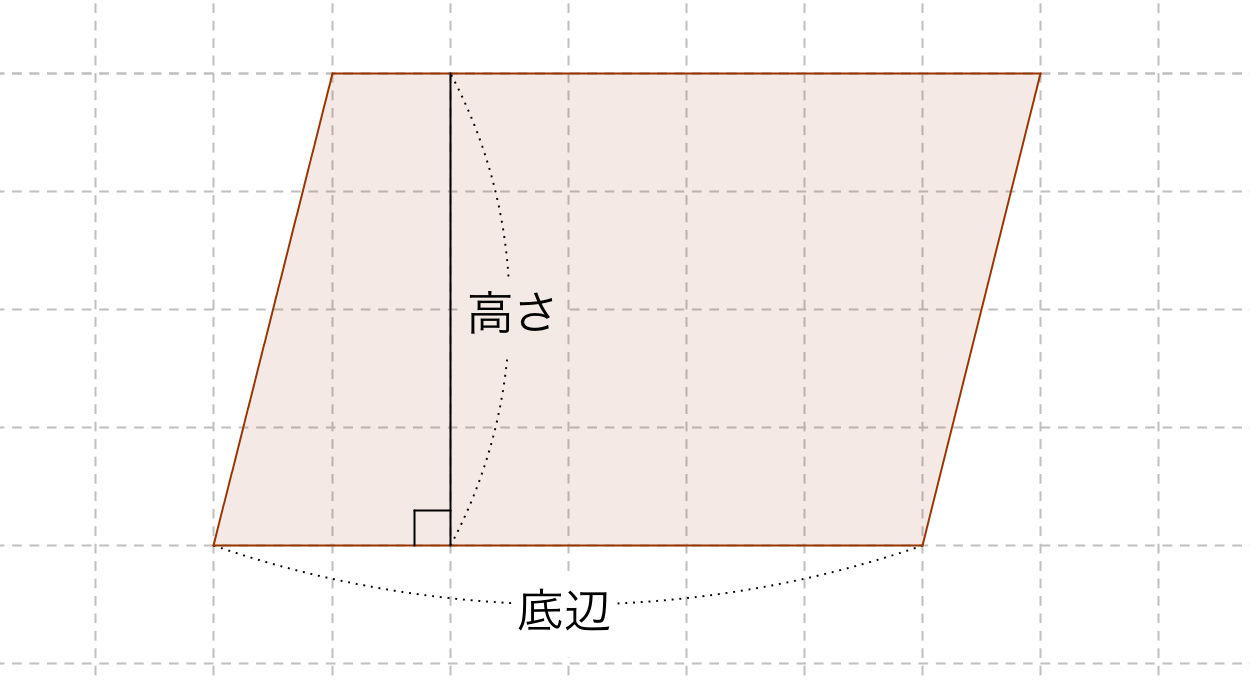
中学数学 平行四辺形の高さの2つの求め方 Qikeru 学びを楽しくわかりやすく




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生




すきるまドリル 小学5年生 算数 図形の面積 無料学習プリント すきるまドリル 無料学習プリント



平行四辺形の面積の公式 算数の公式



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生




中学受験算数 平行四辺形の面積を求める問題 Okwave
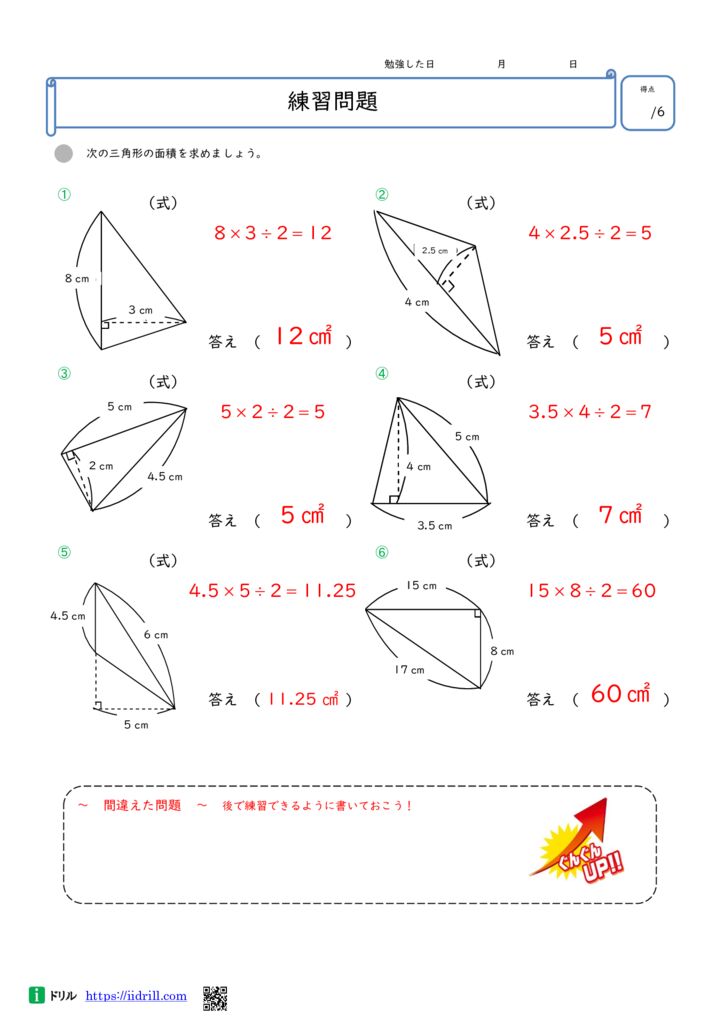



5年生算数ドリル 面積
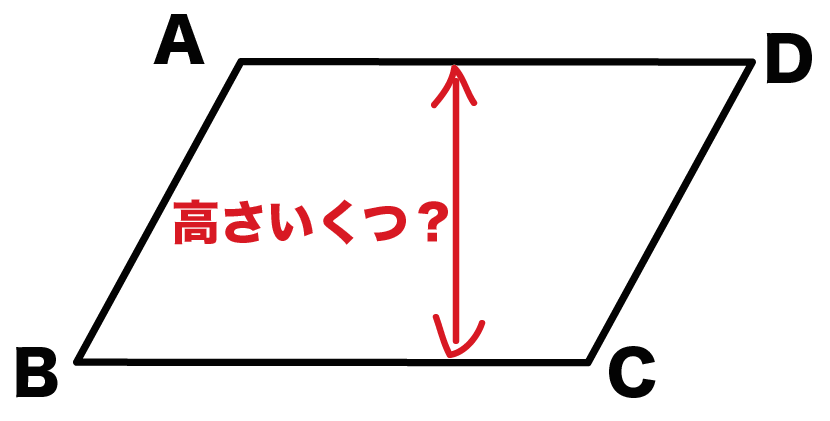



中学数学 平行四辺形の高さの2つの求め方 Qikeru 学びを楽しくわかりやすく



5年生算数ドリル 面積



算数 平面図形と比 1 中学受験 ベネッセ教育情報サイト



1
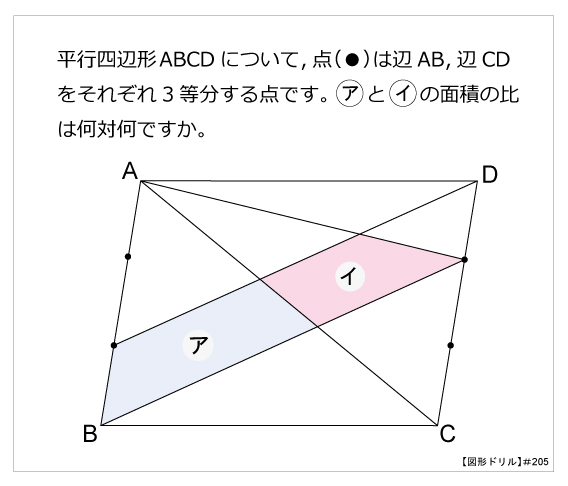



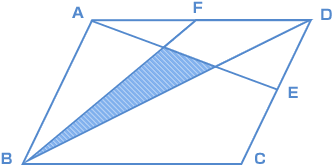
図形ドリル 第5問 平行四辺形内の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦




算数パズル 10秒で解けますか 公式を使わない平行四辺形の面積問題 Youtube




平行四辺形の面積を求める公式 あまり知られていないかも 中学や高校の数学の計算問題
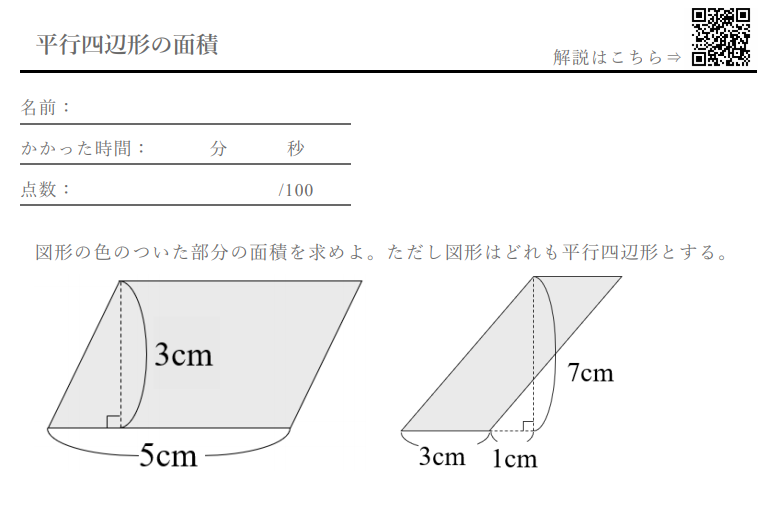



平行四辺形 の面積 計算ドリル 問題集 数学fun
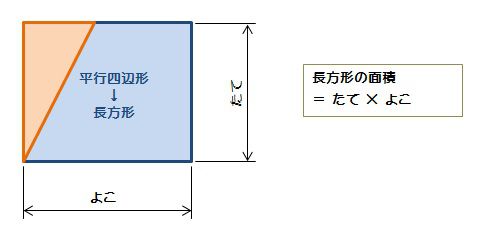



平行四辺形の面積 算数の公式覚えてますか




相似 平行四辺形と面積比の問題を徹底解説 数スタ




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ
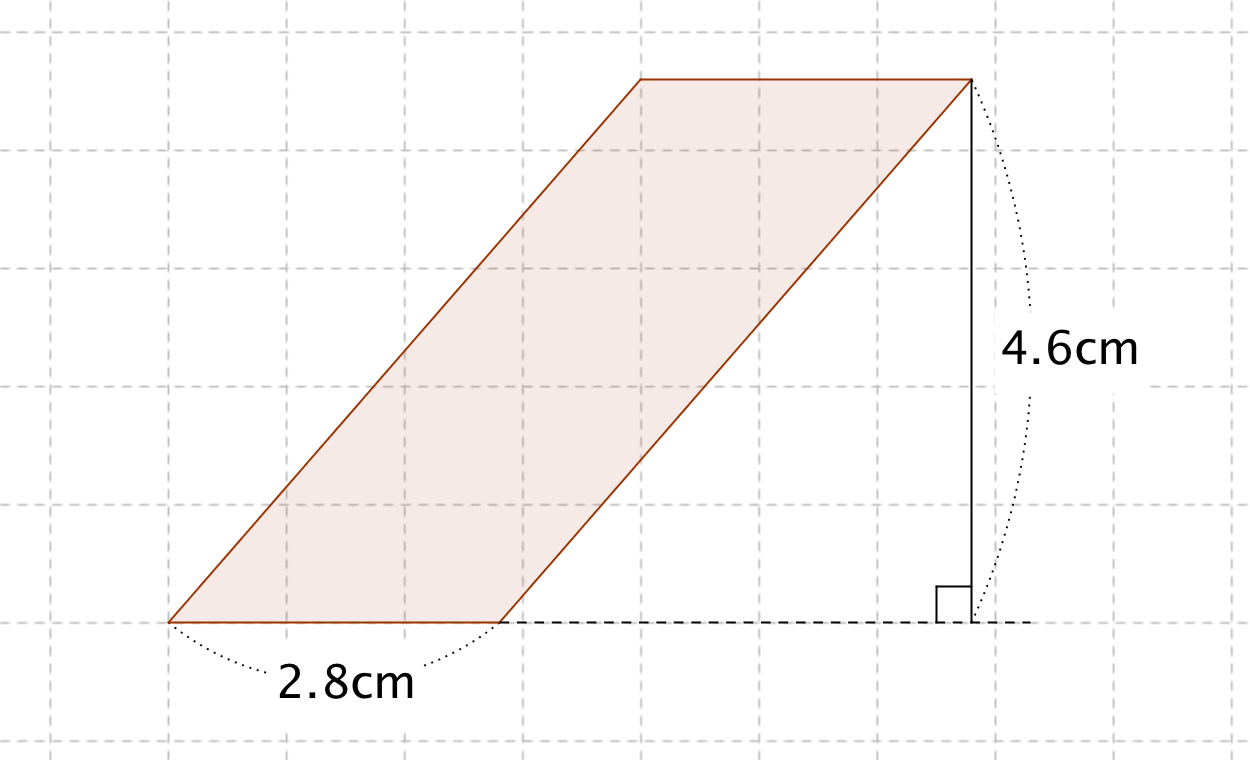



平行四辺形の面積の公式 算数の公式




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun



1
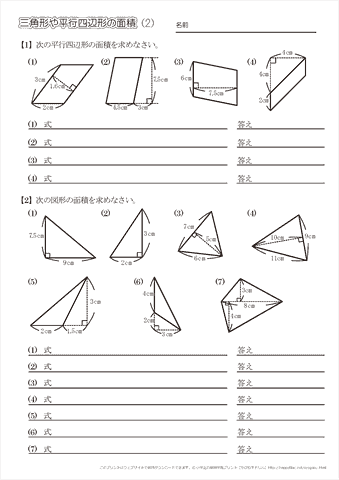



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生
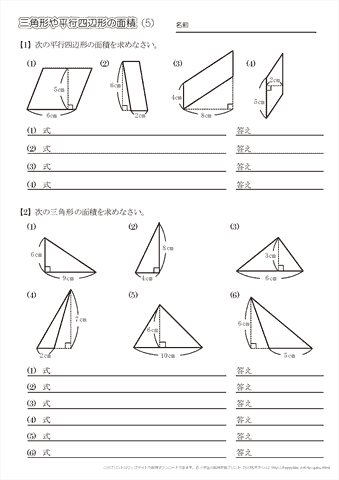



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生




無料 中2数学 発展問題 解答プリント 233 平行四辺形4



5年 平行四辺形の面積 算数イメージ動画集 大日本図書



数学の問題で分からないので教えてください 図のような平行四辺形abcdで Yahoo 知恵袋



今月の問題 平行四辺形
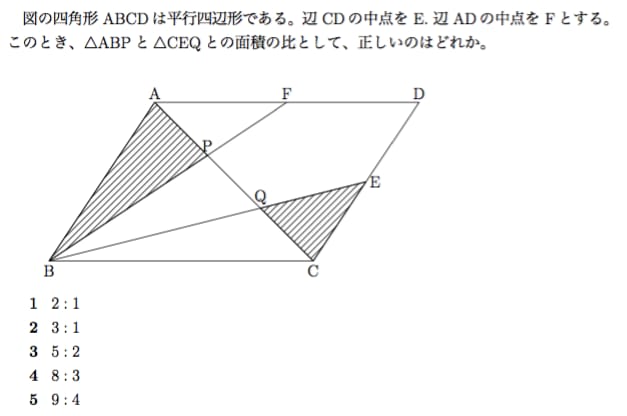



平行四辺形 中点 2つの三角形の面積比 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください



等積変形で難しい面積問題をサクッと解決 平行線と三角形の関係がおもしろい 中学受験ナビ




平行四辺形の面積の求め方 公式と計算例




動画で学習 1 平行四辺形の面積の求め方 算数



ブンブンぱぁとなぁweb 子供の考える力 書く力はこうすれば伸びる




簡単公式 平行四辺形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




平行四辺形の面積の求め方 公式と計算例




小5 算数 小5 41 平行四辺形の面積 Youtube




質問させていただきます Ab Ad 2 3である 三角形apqの面積と平 Okwave



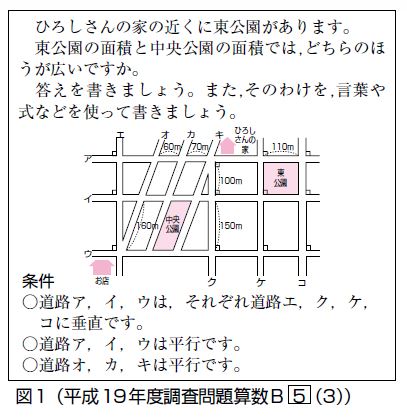
面積 平行四辺形の面積の変わった求め方の問題 数学の要点まとめ 練習問題一覧




平行四辺形のなかの三角形の相似や角度 長さ 等しい面積の求め方 現役塾講師のわかりやすい中学数学の解き方




平行四辺形の面積の求め方 公式と計算例
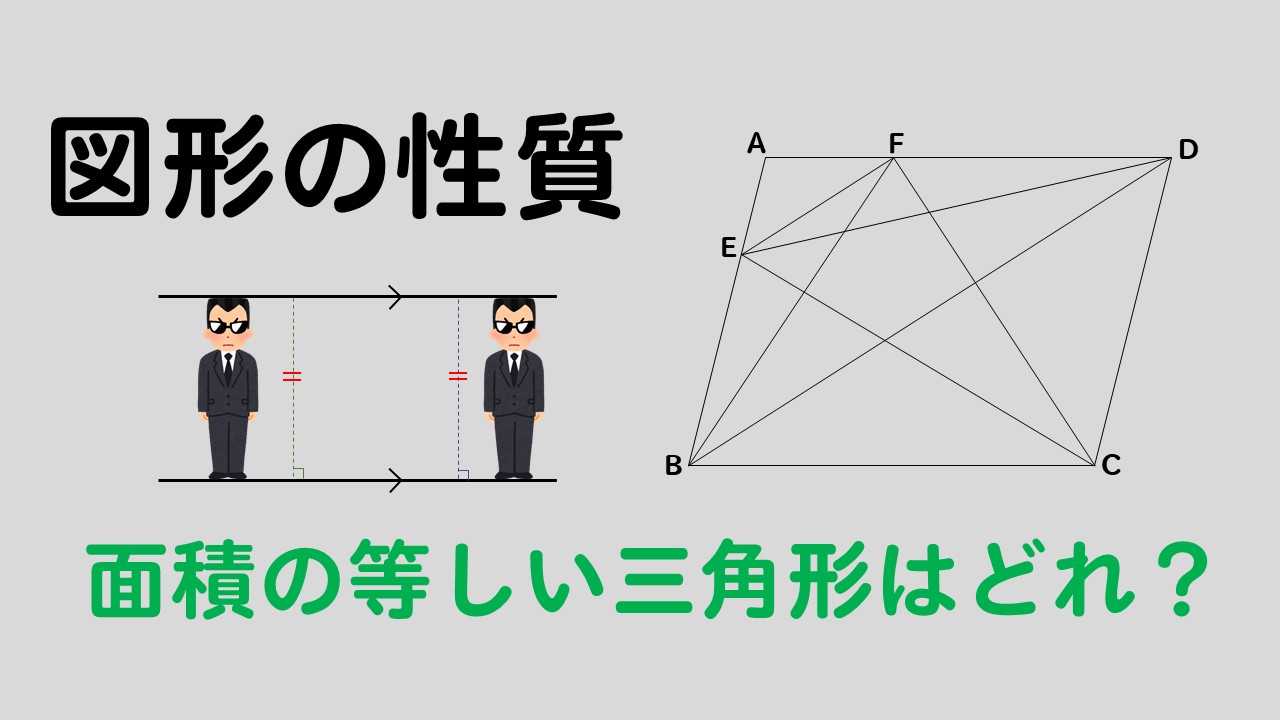



中2数学 平行四辺形の中から面積の等しい三角形を見つける問題を解説 数スタ
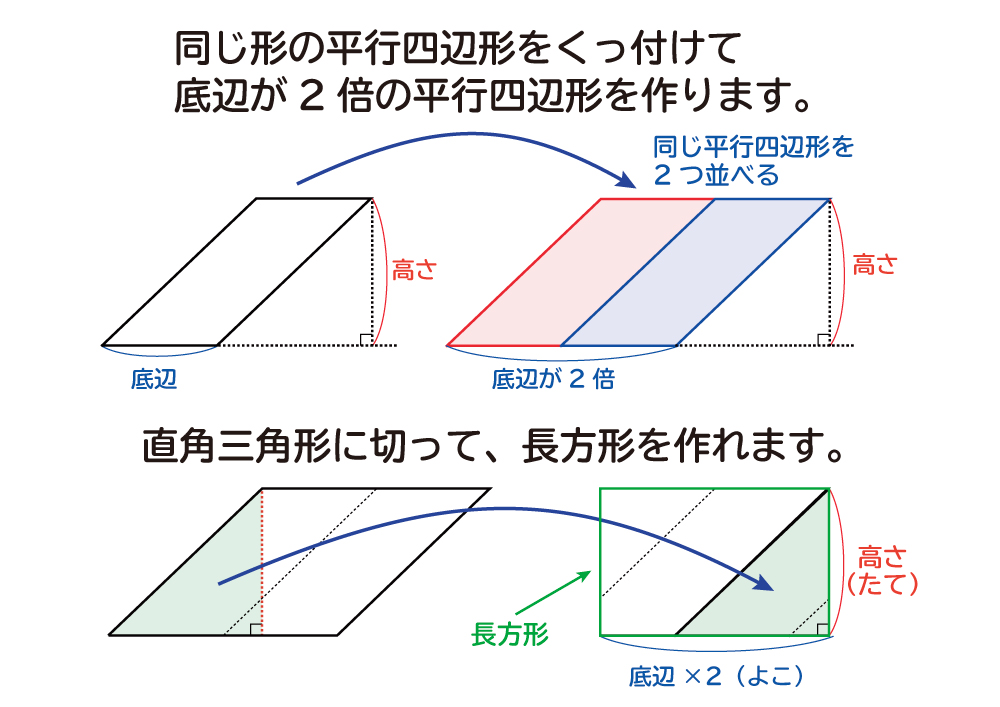



なぜ 平行四辺形の面積は 底辺 高さ なのか を説明します おかわりドリル
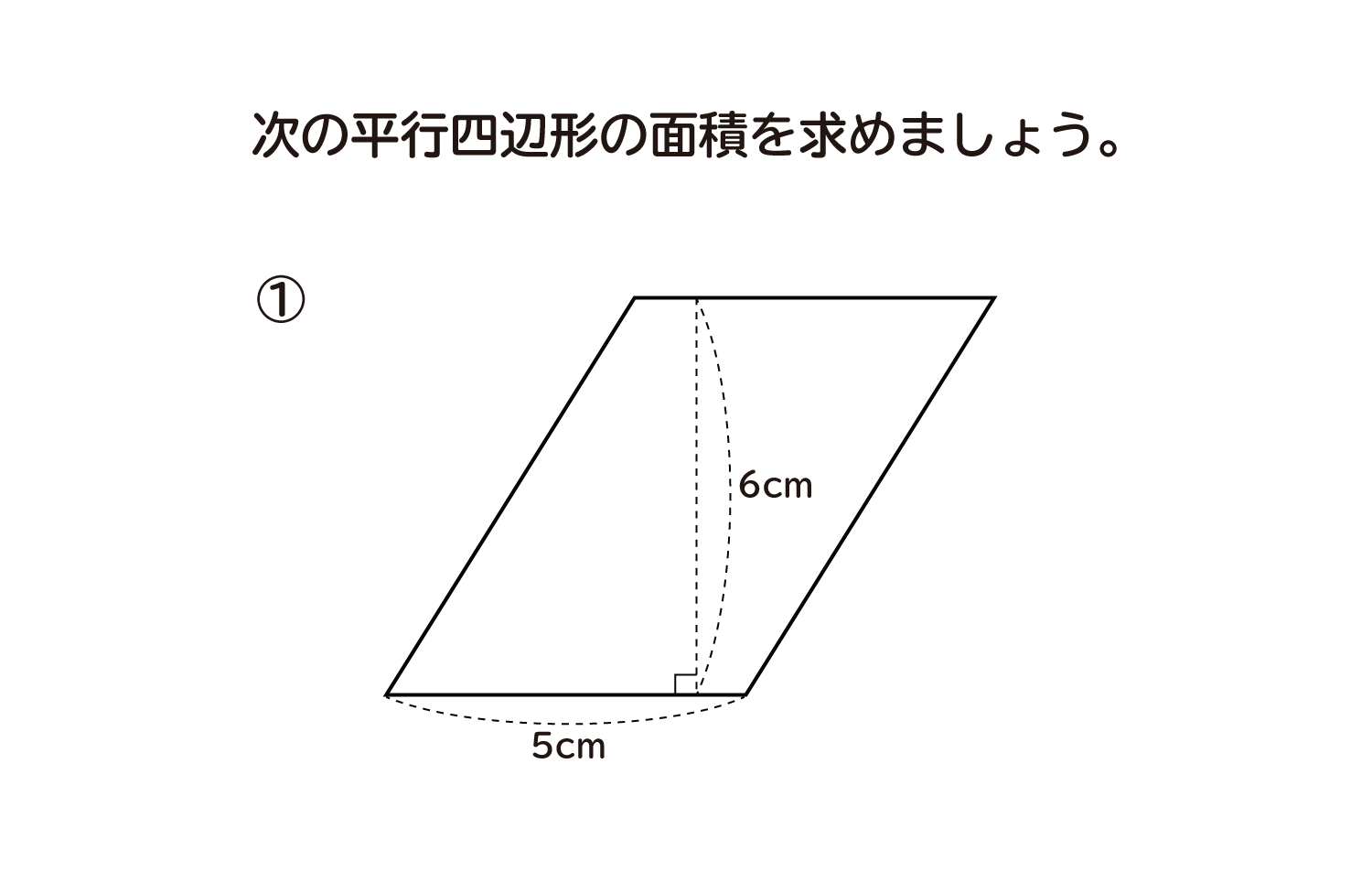



小学5年生 算数 無料問題集 平行四辺形の面積 おかわりドリル



数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
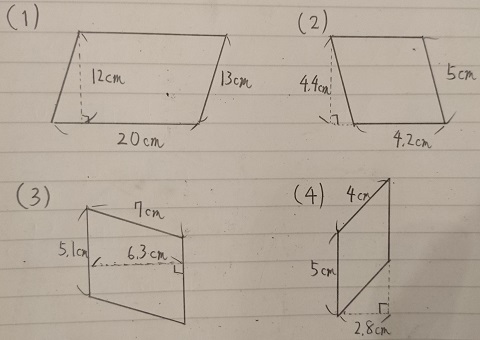



平行四辺形の面積 算数 一般常識クイズ一問一答問題まとめ




関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ
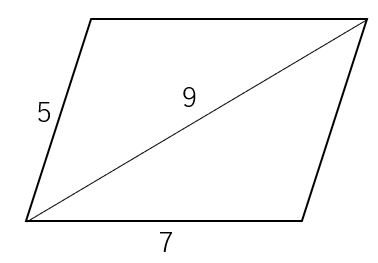



面積 平行四辺形の面積の変わった求め方の問題 数学の要点まとめ 練習問題一覧



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生
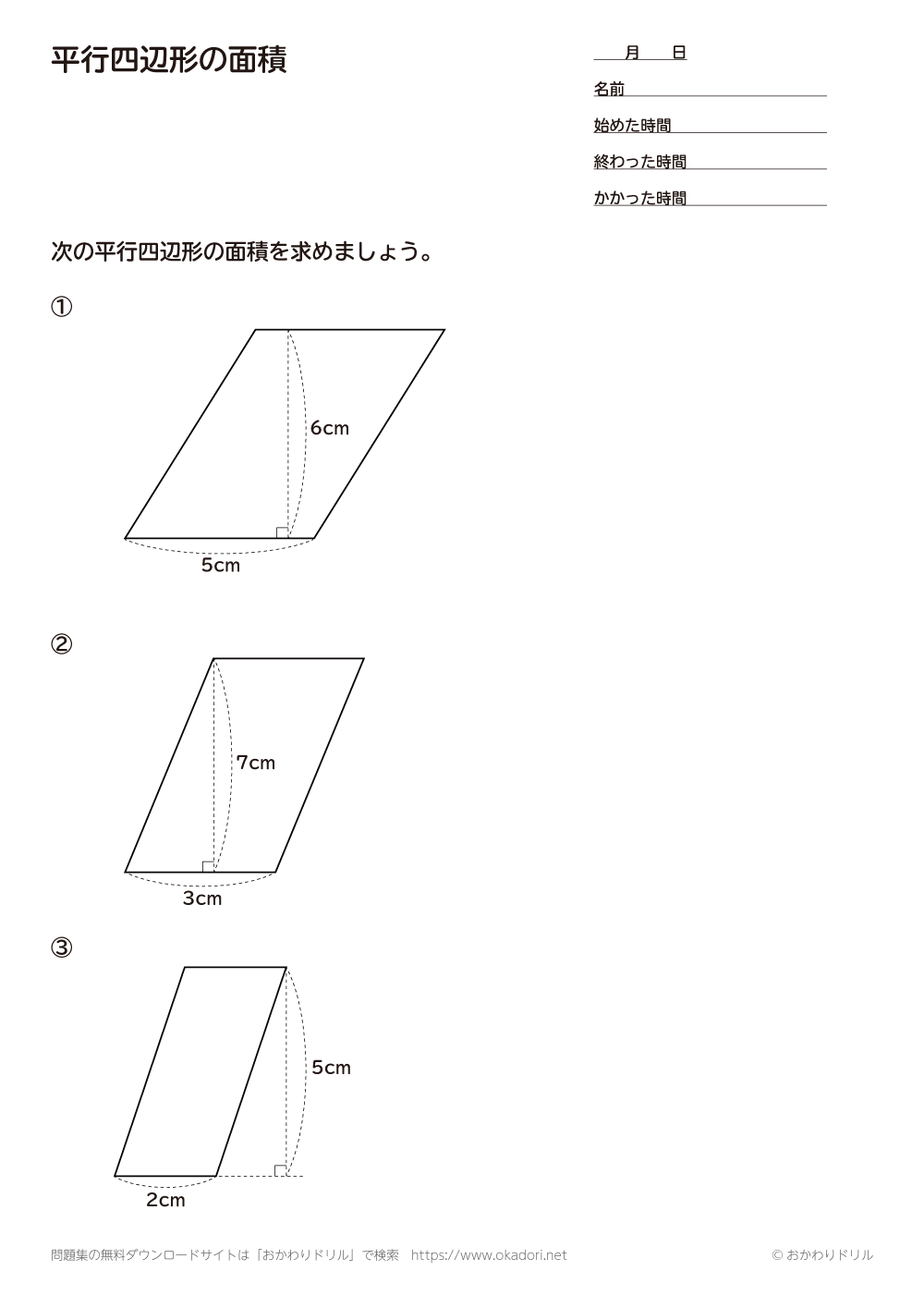



小学5年生 算数 無料問題集 平行四辺形の面積 おかわりドリル
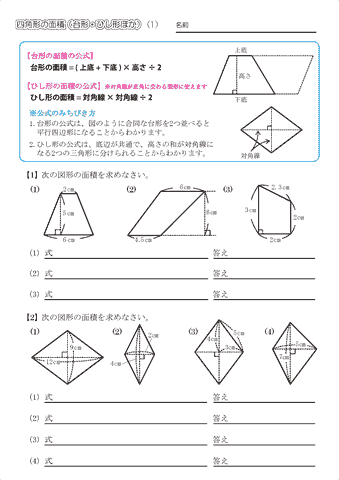



小学5年生の算数 四角形の面積 台形 ひし形ほか 問題プリント ちびむすドリル 小学生




平行四辺形の面積の求め方 公式と計算例



座標平面に描かれた図形に関する問題 バカでもわかる 中学数学
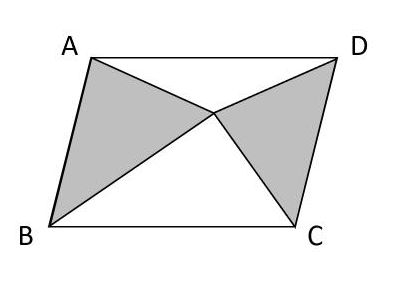



等積変形で難しい面積問題をサクッと解決 平行線と三角形の関係がおもしろい 中学受験ナビ
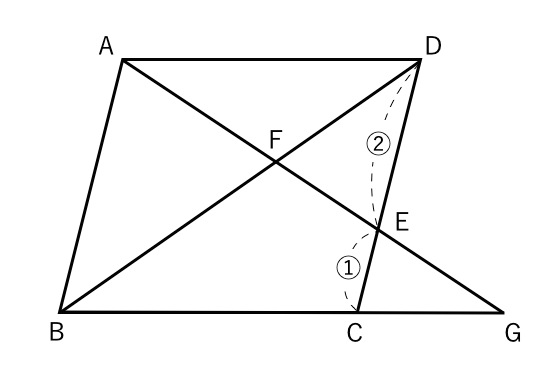



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に




平方四辺形の面積 小5の問題です 斜線部の面積を求めます 答えは14 小学校 教えて Goo
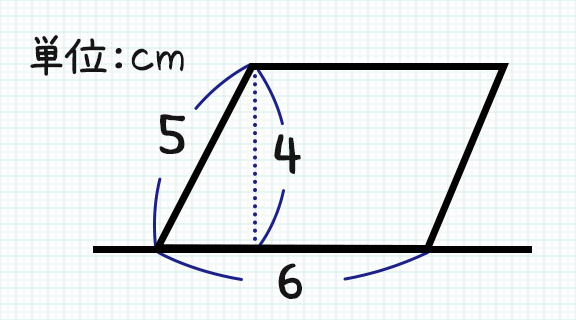



毎日脳トレ この平行四辺形の面積わかる Dアプリ レビュー




公式なんて覚えない ひし形の面積は直感的に考えよう




面積問題 小学4から6年生 算数問題プリント



0 件のコメント:
コメントを投稿